Trees
Trees are typically implemented using a Node/link data structure like that of a linked list.
It has the ability to classify data and separate it reducing the overhead of search.
Terminology
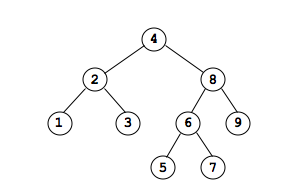
Node: the thing that store the data within the tree . (each circle in the above diagram is a node)Root Node: the top most node from which all other nodes come from. A is the root node of the tree.Subtree: Some portion of the entire tree, includes a node (the root of the subtree) and every node that goes downwards from there. A is the root of the entire tree. B is the root of the subtree containing B,D,E and FEmpty trees: A tree with no nodesLeaf Node: A node with only empty subtrees (no children) Ex. D,E,F,I,J,and G are all leaf nodesChildren: the nodes that is directly 1 link down from a node is that node's child node. Ex. B is the child of A. I is the child of HParentthe node that is directly 1 link up from a node. Ex. A is parent of B. H is the parent of ISibling: All nodes that have the same parent node are siblings Ex. E and F are siblings of D but H is notAncestor: All nodes that can be reached by moving only in an upward direction in the tree. Ex. C, A and H are all ancestors of I but G and B are not.DescendantsorSuccessorsof a node are nodes that can be reached by only going down in the tree. Ex. Descendants of C are G,H,I and JDepth: Distance from root node of tree. Root node is at depth 0. B and C are at depth 1. Nodes at depth 2 are D,E,F,G and H. Nodes at depth 3 are I and JHeight: Total number of nodes from root to furthest leaf. Our tree has a height of 4.Path: Set of branches taken to connect an ancestor of a node to the node. Usually described by the set of nodes encountered along the path.Binary tree: A binary tree is a tree where every node has 2 subtrees that are also binary trees. The subtrees may be empty. Each node has a left child and a right child. Our tree is NOT a binary tree because B has 3 children.
Binary Search Tree (BST)
Binary trees where all values in the left subtree < in the right subtree.
Note
allows us to quickly perform a search on a linking structure
Insertion
To insert into a binary search tree, we must maintain the nodes in sorted order.
Removal
we must be sure to link up the subtree(s) of the node properly
Traversals
As it goes through each node exactly 1 time, the runtime should not exceed O(n) Examples of traversal: print, copy, destroy the structure
Types of traversal:
- depth first,
- breadfirst
Depth First Traversals
3 ordering methods for depth first traversals:
- preorder
- visit a node
- visit its left subtree
- visit its right subtree
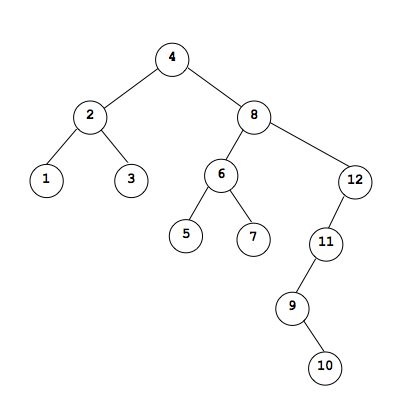
4, 2, 1, 3, 8, 6, 5, 7, 12, 11, 9, 10
- inorder
- visit its left subtree
- visit a node
- visit its right subtre
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 (resutls in sorted order)
- postorde
- visit its left subtree
- visit its right subtree
- visit a node
1, 3, 2, 5, 7, 6, 10, 9, 11, 12, 8, 4 (used to destroy)
-PreOrder
void preOrderPrint(const Node* subtree) const{
//base case is we have an empty tree... in that case we do nothing
//and exit the function
if(subtree!=nullptr){
//print value in current node
std::cout << subtree->data_ << std::endl;
//print left subtree
preOrderPrint(subtree->left_);
//print right subtree
preOrderPrint(subtree->right_);
}
}
public:
...
void preOrderPrint() const {
preOrderPrint(root_);
}
- InOrder
void inOrderPrint(const Node* subtree) const{
//base case is we have an empty tree... in that case we do nothing
//and exit the function
if(subtree!=nullptr){
//values in left_ are smaller, we need to print them all first
inOrderPrint(subtree->left_);
//print value in current node
std::cout << subtree->data_ << std::endl;
//values in right_ are bigger, we need to print them all after we
//print current node
inOrderPrint(subtree->right_);
}
}
public:
...
void inOrderPrint() const {
inOrderPrint(root_);
}
- PostOrder (Destructor)
void destroy(Node* subtree){
//base case is we have an empty tree... in that case we do nothing
//and exit the function
if(subtree!=nullptr){
destroy(subtree->left_);
destroy(subtree->right_);
delete subtree;
}
}
public:
...
~BST(){
destroy(root_);
}
Breadth-First Traversal
going through all nodes from the root, then all its children then all of its children's children, etc. level by level
4, 2, 8, 1, 3, 6, 12, 5, 7, 11, 9, 10
Implementation
- binary search tree is made up of nodes
- Each node can have a left or right child
- Empty trees are represented as nullptrs
- data stored in the nodes must be of some type that is comparable
template <typename T>
class BST{
struct Node{
T data_;
Node* left_;
Node* right_;
Node(const T& data, Node* left=nullptr, Node* right=nullptr){
data_=data;
left_=left;
right_=right;
}
};
//single data member pointing to root of tree
Node* root_;
public:
BST(){
root_=nullptr;
}
void insert(const T& data){...}
bool search(const T& data) const {...}
void breadthFirstPrint() const {...}
void inOrderPrint() const {...}
void preOrderPrint() const {...}
~BST(){...}
};
Insert
(iteration ver)
void insert(const T& data){
if(root_==nullptr){
root_=new Node(data);
}
else{
bool isInserted=false; //set to true when once we insert the node
Node* curr=root_; //used to iterate through nodes
while(!isInserted){
if(data < curr->data_){
//data belongs in left subtree because it is
//smaller than current node
if(curr->left_){
//there is a node to the left so go left
curr=curr->left_;
}
else{
//there isn't a node to left
//create a node to the left
curr->left_=new Node(data);
isInserted=true;
}
}
else{
//data belongs in right subtree.
if(curr->right_){
//there is a node to the right so go right
curr=curr->right_;
}
else{
//there isn't a node to right
//create a node to the right
curr->right_=new Node(data);
isInserted=true;
}
}
}
}
}
(recursive ver)
void insert(const T& data, Node*& subtree){
//NOTE: the & after Node* is really important for this. It makes
//subtree another name for whatever you pass in. For example, if
//in the initial call from non-recursive insert(), we pass in root_
//subtree is actually another name for root_ itself. Not just a copy
//of data in the root. This means that when we change subtree, we
//are actually changing root.
if(subtree==nullptr){
//if tree is empty, make subtree point to the new node
subtree=new Node(data);
}
else if (data < subtree->data_){
//if data is smaller than data in subtree's root
//insert it to the left.
insert(data,subtree->left_);
}
else{
//otherwise its bigger so we insert it into the right subtree
insert(data,subtree->right_);
}
}
void insert(const T& data){
insert(data,root_);
}
Search
Note
should never look at the entire tree
(iteration ver)
bool search(const T& data) const {
Node* curr=root_; //used to iterate through tree
bool found=false; //true if we find it false if we haven't yet
//loop until we either find it or we have no more tree
while(!found && curr){
if(data==curr->data_){
found=true;
}
else if(data < curr->data_){
curr=curr->left_;
}
else{
curr=curr->right_;
}
}
return found;
}
(recursive)
bool search(const T& data, const Node* subtree) const{
bool rc=false;
//if it tree is empty, the if is skipped and we return false
if(subtree != nullptr){
if(data == subtree->data_){
//base case 2: we find it in the root of subtree
rc=true;
}
else if(data < subtree->data_){
//data is smaller than that stored in root. If we find it,
//it will be in left subtree, so we call search to see if its
//there and return the result
rc=search(data,subtree->left_);
}
else{
//otherwise its bigger, use the search() function
//to see if its in right subtree and return the result
rc=search(data,subtree->right_);
}
}
return rc;
}
public:
bool search(const T& data) const{
//call and return result from recursive search() function
return search(data,root_);
}
Breadth First Print
use the queue data structure to order what nodes to deal with next
void breadthFirstPrint() const{
Queue<Node*> theNodes; //we assume the queue class has these functions
//enqueue(), dequeue(), front(), isEmpty()
//prime queue
if(root_){
theNodes.enqueue(root_);
}
//while we have nodes to deal with
while(!theNodes.isEmpty()){
//deal with first node and remove it from queue
Node* curr=theNodes.front();
theNodes.dequeue();
if(curr->left_){
//if the current node has a left child add it to queue
theNodes.enqueue(curr->left_);
}
if(curr->right_){
//if the current node has a right child add it to queue
theNodes.enqueue(curr->right_);
}
//print the current node's data
std::cout << curr->data_ << " ";
}
std::cout << std::endl;
}