Graphs

A graph is made up of a set of vertices and edges that form connections between vertices. If the edges are directed, the graph is sometimes called a digraph.

Terminology

• adjacent - Given two nodes A and B. B is adjacent to A if there is a connection from A to B. In a digraph if B is adjacent to A, it doesn't mean that A is automatically adjacent to B.
• edge weight/edge cost - a value associated with a connection between two nodes
• path - a ordered sequence of vertices where a connection must exist between consecutive pairs in the sequence.
• simplepath - every vertex in path is distinct
• pathlength - number of edges in a path
• cycle - a path where the starting and ending node is the same
• strongly connected - If there exists some path from every vertex to every other vertex, the graph is strongly connected.
• weakly connect - if we take away the direction of the edges and there exists a path from every node to every other node, the digraph is weakly connected.

Rrepresentation

1. Adjacency Matrix

• 2 dimensional array. Each index value represents a node.

2. Adjacency List

• uses an array of linked lists to represent a graph Each element represents a vertex. For each vertex it is connected to, a node is added to it's linked list. For graphs with weights each node also stores the weight of the connection to the node. Adjacency lists are much better if the graph is sparse.

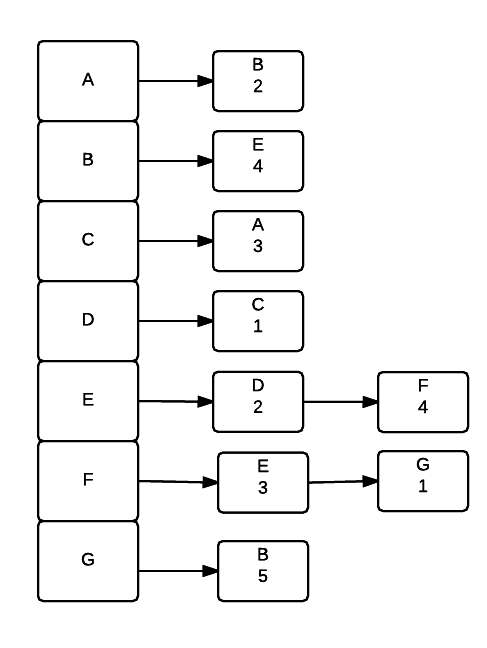
Dijkstra's Algorithm

Dijkstra's Algorithm is an algorithm for finding the shortest path from one vertex to every other vertex. This algorithm is an example of a greedy algorithm.

Greedy algorithms are algorithms that find a solution by picking the best solution encountered thus far and expand on the solution.

The general algorithm can be described as follows:

1. Start at the chosen vertex (we'll call it v1)
2. Store the cost to travel to each vertex that can be reached directly from v1.
3. Next look at the vertex that is least costly to reach from v1 (we'll call this vertex v2 for this examples
4. For each vertex that is reachable from v2, find the total cost to that vertex starting from v1 (we want the total cost, not just the lowest cost from v2). Update the cost of travel to these vertices if it is lower than the current known cost.
5. Pick the next lowest cost and continue.