Sorting

Sorting is the process of taking a set of data and creating an ordering based on some criteria. The criteria must allow for items to be compared and used to determine what should come first and second.

Simple Sorts

1. Bubble Sort
2. Insertion Sort
3. Selectino Sort

Bubble Sort

Bubble sort is called bubble sort because the algorithm repeated bubbles the largest item within the list to the back.

Algorithm

1. start with first pair of numbers
2. compare them and if they are not correctly ordered, swap them
3. go through every pair in list doing the above 2 steps
4. repeat the above 3 steps n-1 times (ie go through entire array n-1 times) and you will sort the array

void bubbleSort(int arr[],int size){
    int tmp;                          /*used for swapping*/
    int i;
    int j;
    for (i=0; i<size-1; i++) {
        for (j=0; j<size-1-i; j++){
            int next = j+1;
            if (arr[next] < arr[j]) {          /* compare the two neighbors */
                tmp = arr[j];                   /* swap a[j] and a[j+1]      */
                arr[j] = arr[next];
                arr[next] = tmp;
            }
        }
    }
}

T(n) is O(n^2)

Insertions Sort

Insertion sort is called insertion sort because the algorithm repeated inserts a value into an array that is already sorted.
It essentially chops the array into two pieces. The first piece is sorted, the second is not.
We repeatedly take a number from the second piece and insert it into the already sorted first piece of the array.

Algorithm

1.start with second variable. 2.put number into a temporary variable. This makes it possible to move items into the spot the number use to occupy. This spot is now considered to be an empty spot in the sorted portion of the array 3.if number in temporary can go into empty spot, put it in 4.otherwise move last item in the part into empty spot 5.repeat steps 3 to 4 until item is temp is placed into the first part of the array 6.repeat for every number in the second part of the array until all numbers are placed

void insertionSort(int arr[],int size){
    int curr;
    int i, j;
    for(i=1;i<size;i++){
        curr=arr[i];
        for(j=i;j>0 && arr[j-1] > curr;j--){
            arr[j]=arr[j-1];
        }
        arr[j]=curr;
    }
}

Selection Sort

Selection sort works by selecting the smallest value out of the unsorted part of the array and placing it at the back of the sorted part of the array.

Algorithm

1. find the smallest number in the between index 0 and n-1 2.swap it with the value at index 0 3.repeat above 2 steps each time, starting at one index higher than previous and swapping into that position

void selectionSort(int arr[],int size){
    int i,j;
    int min;  //index of smallest value in the unsorted array

    for(int i=0;i<size-1;i++){
        min=i;
        for(int j=i+1;j<size;j++){
            if(arr[j] < arr[min]){
                min=j;
            }
        }
        if(min!=i){
            int tmp=arr[min];
            arr[min]=arr[i];
            arr[i]=tmp;
        }
    }
}

Merge Sort

The merge sort works on the idea of merging two already sorted lists. If there existed two already sorted list, merging the two together into a single sorted list can be accomplished in O(n) time.

Algorithm

1. Have a way to "point" at the first element of each of the two list
2. compare the values being pointed at and pick the smaller of the two
3. copy the smaller to the merged list, and advance the "pointer" of just that list to the next item.
4. Continue until one of the list is completely copied then copy over remainder of the rest of the list

template <class TYPE>
void mergeSort(vector<TYPE>& arr, vector<TYPE>& tmp, int start, int end){
  if (start<end){
    int mid=(start+end)/2;
    mergeSort(arr,tmp,start,mid);
    mergeSort(arr,tmp,mid+1,end);
    merge(arr,tmp,start,mid+1,end);
  }
}

template <class TYPE>
void merge(vector<TYPE>& arr, vector<TYPE>& tmp, int start,
	int start2, int end){
	int aptr=start;
	int bptr=start2;
	int i=start;
	while(aptr<start2 && bptr <= end){
		if(arr[aptr]<arr[bptr])
			tmp[i++]=arr[aptr++];
		else
			tmp[i++]=arr[bptr++];
	}
	while(aptr<start2){
		tmp[i++]=arr[aptr++];
	}
	while(bptr<=end){
		tmp[i++]=arr[bptr++];
	}
	for(i=start;i<=end;i++){
		arr[i]=tmp[i];
	}
}

T(n) is O(n)

Quick Sort

This sort is fast and does not have the extra memory requirements of MergeSort.

On average its run time is O(nlogn) but it does have a worst case run time of O(n^2)

Algorithm

1.Pick a value from the array as the pivot 2.Let i=front, j= back 3.advance i until you find a value arr[i] > pivot 4.move j towards front of array until arr[j] < pivot 5.swap these arr[i] and arr[j]. 6.repeat step 3 to 5 until i and j meet 7.The meeting point is used to break the array up into two pieces 8.QuickSort these two new arrays

template <class TYPE>
void QuickSort(vector<TYPE>& arr, int left, int right){
  if(right-left <=3){
    InsertionSort(arr,left,right);
  }
  else{
    int pivotpt=right;
    int i=left;
    int j=right-1;
    TYPE pivot=arr[pivotpt];
    while(i<j){
      while(arr[i]<pivot) i++;
      while(arr[j]>pivot) j--;
      if(i<j)
        swap(arr[i++],arr[j--]);
    }
    swap(arr[i],arr[pivotpt]);
    QuickSort(arr,left,i-1);
    QuickSort(arr,i+1,right);
  }
}

template <class TYPE>
void QuickSort(vector<TYPE>& arr){
  QuickSort(arr,0,arr.size()-1);
}

Heap and Heap Sort

Heap Sort is a sort based on the building and destroying of a binary heap. The binary heap is an implementation of a Priority Queue.

Basic Operations

• insert - add an item to the binary heap
• delete - removes the item with the highest priority in the binary heap

Priority Queue

A priority queue is similar to a queue in that you use it for ordering data. However, instead of ordering based on when something was added, you order it based on the priority value of the item. An item at the front of the priority queue is the item with the highest priority.

Binary Heap

Binary Heap - A binary heap is a complete binary tree where the heap order property is always maintained.

Binary Tree - A binary tree is either a) empty (no nodes), or b) contains a root node with two children which are both binary trees.

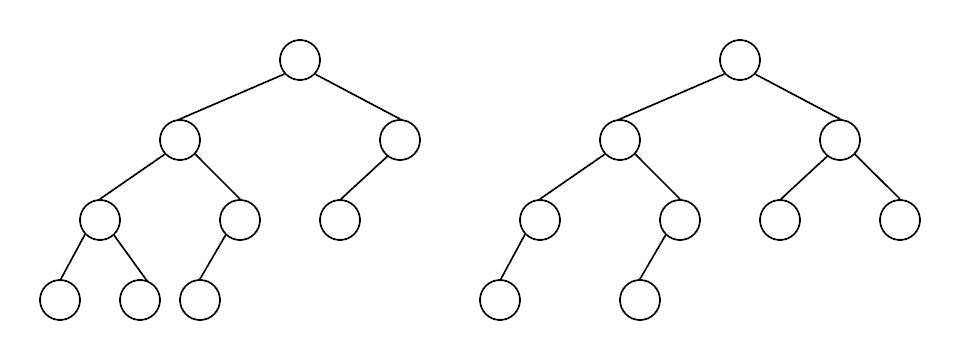
Complete Binary Tree - A binary tree where there are no missing nodes in all except at the bottom level. At the bottom level the missing nodes must be to the right of all other nodes

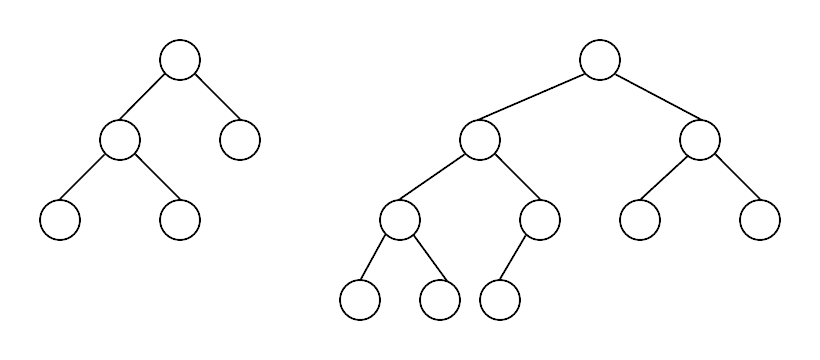
These binary trees are not complete. The first one is missing a node one level higher than leaves, the second is missing further left in the tree than an existing node

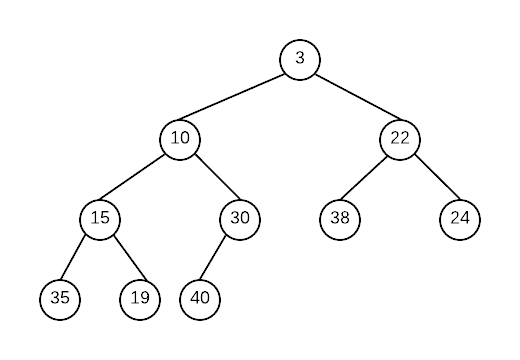
Heap Order Property

For each node, the parent of the node must have a higher priority, while its children must have a lower priority.

Note

need to add heapify